Gerhard Kubik - Andreas Reisenbauer - Afrikanische Rhythmen

Downladen des Programmquelltextes HIER

Zyklisches (=periodisches Patternproblem) 1

Ein 12-Sessel-Rundtisch soll von 5 Menschen besetzt werden, wobei diese ununterscheidbar und die Numerierung der Plätze ebenfalls unerheblich sein soll. (è alle Lösungen durch 12, weil Drehung um 30° Ähnlichkeitstransformation ist und somit keine neue Lösung schafft)

Sie sollen jeweils keinen Platznachbarn haben.

LÖSUNGSWEG 1 (mittels Pattern)

x Sessel besetzt o Sessel leer

A xo B xoo C xoo D xoooo …..

Durch geschickte Aneinanderreihung der Pattern soll die Summe(x+o)=12, Summe(x)=5 und zugleich Summe(o)=7 sein.

D(x1/o4/s5) da für alle Patterns o >= x à S(x5/o>=8/s>12) geht nicht.

C(x1/o3/s4) da für alle Patterns o >= x à S(x5/o>=7/s>12) geht nur mit

AAAAC : W = 5! / (4!.1!) = 5

aus symmetrischen Gründen muss durch 5 (Drehen) geteilt

werden à W=1

B(x1/o2/s3) à es fehlen 4x und 5o, dies ist nur mit B+3A zu bewerkstelligen

AAABB: W=5!/(3!.2!)=10

aus symmetrischen Gründen muss durch 5 (Drehen) geteilt

werden à W=2

-à es gibt 3 verschiedene Lösungen: AAABB, AABAB, AAAAC

also:

xoxoxoxooxoo, xoxoxooxoxoo, xoxoxoxoxooo

LÖSUNGSWEG 2 (Kombionatorisch)

Erreichbar durch 5 A=xo und 2 B=o frei verteilbar: 7!/2!/5! = 21, davon 7 verschiedene Drehungen möglich à 3 Möglichkeiten: BBAAAAA BABAAAA BAABAAA

LÖSUNGSWEG 3 mittels COMPUTERprogramm (siehe hinten):

Theoretisch zu überprüfende mögliche Konfiguartionen: W=12! / (5! 7!) = 792:

Zyklisches (=periodisches Patternproblem) 2

Es gibt 7 Gäste, jeweils 2 Paare dürfen beieinander sitzen, sonst sind nur Einzelsitzende erlaubt.

LÖSUNGSWEG 1 als Umkehrlösung von oben AAABB; AABAB mint A=xxo und B=xo

LÖSUNGSWEG 2 mittels COMPUTERprogramm (siehe hinten):

LÖSUNGSWEG 3 mittels PATTERN

A xo B xxo C xoo D xooo E xoooo F xooooo G xxoo H xxooo I xxoooo J xxooooo

K xx usw. geht nicht weil nur x und xx erlaubt sind (max. Paare) und zwar 2

gesucht also: Summe(x+o)=12, Summe(o)=5 und Summe(x)=7 wobei Summe(xx)=2.

Also ohne Einschränkung der Allgemeinheit: Beginnen mit E, F, I und J vergibt zu viele o:

H (x2,o3,s5) +A+B = x5 o5(ok) s10 geht nicht!

G (x2,o2,s4) +B+2A = x6 o5(ok) s11 geht nicht!

D (x1,o3,s4) + 2B = x5 o5(ok) s10 geht nicht!

C (x1o2,s3) +2B +A= x6 o5 (ok) s11 geht nicht!

ab jetzt nur mehr A und B verwendbar: à 2B3A => BBAAA und BABAA

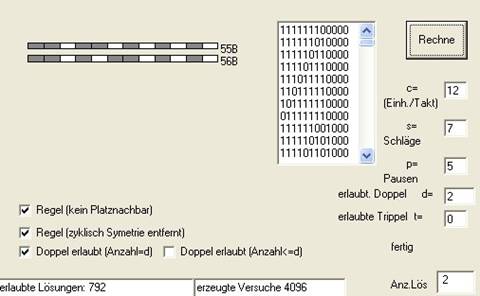
LÖSUNGSWEG 2 mittels COMPUTERprogramm:

Durch Automatenzählrpoutine werden alle Varianten allgemein erzeugt, d.h. nicht beschränkt auf 12/5/7. Danach (nach Auswahl):

Symmetrien (Drehung) werden entfernt.

Durch Nebenbedingungen werden ungültige ausgeschlossen.